1. Invest-Safely.com
    2. >>
  2. Personal Finance Goals
    3. >>
  3. Personal Money Management

Witness the Power of Compounded Returns using the following Compound Interest Example

The following, simple compound interest example can go a long way in explaining the power of this fundamental financial concept.

Some people have even claimed that when Albert Einstein was asked to name the greatest invention in human history, he simply replied "compound interest". [Hartgill, 1997]

What is Compound Interest?

First, lets start with the concept of "simple" interest. Simple interest refers to the calculation of interest based on the "principle" or initial value.

For example, if you have $10,000 and earn 10% interest per year, the calculation for simple interest is:

    Year 1 = $10,000 x 10% = $1,000 interest payment

    Year 2 = $10,000 x 10% = $1,000 interest payment

    Year 3 = ...

"Compound" interest is the calculation of interest based on the principle AND interest. Lets take the simple interest equation above and turn it into a compound interest example.

If you have $10,000 and earn 10% interest per year, how would you calculate the interest in the second year using compound interest?

    Year 1 = $10,000 x 10% = $1,000 interest payment

    Year 2 = ($10,000 + $1,000) x 10% = $1,100 interest payment

Compounding allows you to earn interest on your interest, so to speak. That is the power of compound interest; you get profit on your profit (coincidentally, this is the 3rd step towards better investing).

The Positive Benefits of Compound Interest

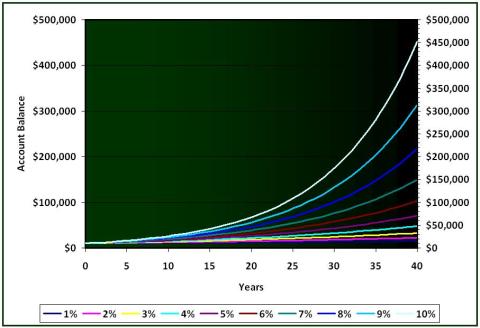
The chart below illustrates the power of compounding, using an initial account balance of $10,000. Each colored line represents a different annual interest rate.

Compound Interest Example - Yearly Compounding of 10000

Compound Interest Example - Yearly Compounding of $10,000
(Click for the full size image)

For each interest rate (see the legend along the bottom of the graph), you can trace how much your balance will rise over a given period of time. If you achieved a constant return of 7%, your account would grow as follows:

    Year 1 = $10,000 + ($10,000 x 7%) = $10,700

    Year 2 = $10,700 + ($10,700 x 7%) = $11,449

    Year 3 = $11,449 + ($11,449 x 7%) = $12,250

    Year 4 = ...

The reason everyone talks about investing for the "long term" is due to compounding returns. You can see how quickly your balance can grow in this compound interest example.

Safe Investing Tip Use the "Rule of 72" to estimate how long it will take to double your money

Divide 72 by your yearly interest rate, and you get the number of years it will take you to double your money.

The real magic happens after your money has been compounding for 20+ years!

The Negative Side of Compounding

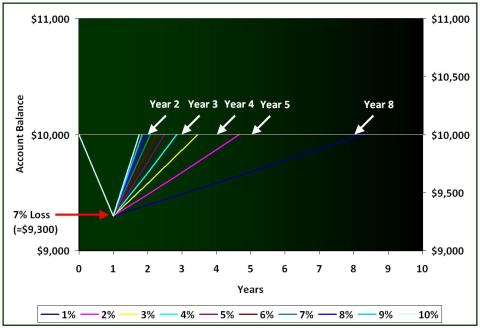
If interest rates are positive, and your money is in some kind of "cash equivalent" investment (CDs, Money Markets, Savings or Interest-bearing checking accounts), all is well. Compounding isn't all rainbows and unicorns though. When you put money into an investment, that money is at risk of loss until you pull it back out. The chart below shows how long it takes to recover from a 7% loss, if you started with $10,000.

Compound Interest Example - Yearly Compounding After 7% Loss

Time Required to Reach $10,000 after a Loss of 7%
(Click for the full size image)

For example, if you lost 7% in Year 1, and then gained 7% in Years' 2 and 3, the calculations are as follows:

    Year 1 = $10,000 + ($10,000 x -7%) = $9,300

    Year 2 = $9,300 + ($9,300 x 7%) = $9,951

    Year 3 = $9,951 + ($9,951 x 7%) = $10,648

You can see that your ability to profit from your profit takes longer when you lose money. This holds true if you cashed out after the loss and put your money in a savings account earning those rates, or, if you kept investing and averaged those rates of return for the year. Now look at the impact of compounding by adding another loss.

If you lost 7% in Year 1, and then another 7% in Year 2, the calculations are as follows:

    Year 1 = $10,000 + ($10,000 x -7%) = $9,300

    Year 2 = $9,300 + ($9,300 x -7%) = $8,649

    Year 3 = $8,649 + ($8,649 x 7%) = $9,254

    Year 4 = $9,254 + ($9,254 x 7%) = $9,902

    Year 5 = $9,902 + ($9,902 x 7%) = $10,595

Now, instead of breaking even in Year 3, you're back above your original balance of $10,000 in Year 5! Hold that thought...lets take this "negative" compound interest example one step further.

The Real Break-Even Point

Technically speaking, the chart above shows you how to get back to your original balance. In other words, if you lost 7% the first year ($700 based on the $10,000 compound interest example graphed above), it would take some time get back to a $10,000 account balance again (sometime in Year's 2 through 9, depending on your rate of return).

But is that really break-even?

No, because your break-even point is NOT $10,000...it's actually something higher, depending on your rate of return.

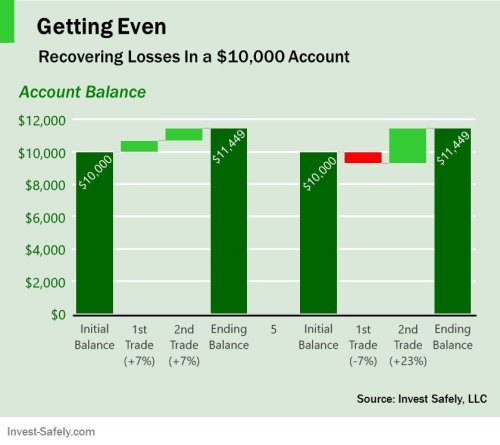
Even though the compound interest examples above are based on an annual interest payment, the same principle holds true when you're buying and selling stocks. Substitute years for "trades", and you can see how quickly losses can pile up. Imagine you have all $10,000 in one investment that loses 7%. You sell, buy another stock, and that one loses 7%. How would you regain what you lost?

Using the 7% loss example, but converting it to "trades", lets find the real break-even.

Compound Interest Example - Yearly Compounding Needed to Break Even

(Click for the full size image)

We know that we could have had $11,449 at after 2 years with a 7% interest rate, compounded annually. The same would be true if we made two trades that returned 7%. And we know that our balance after a 7% loss would be $9,300, from the second example (first chart). So we need to know what rate of return (or interest rate) would be required to turn $9,300 back into $11,449 after 1 trade (or year).

    Year 2 = $9,300 + ($9,300 x ?%)

    Year 2 = $11,449

Combine the two equations:

    $9,300 + ($9,300 x ?%) = $11,449

    ($9,300 x ?%) = $11,449 - $9,300

    ?% = ($11,449 - $9,300)/$9,300

    ?% = 0.23 = 23%

Check that out! You would need to achieve a 23% return on your second trade (or year 2) in order to get reach the "real" break-even had you made money in the first place!

Your Takeaway

Think about this: Many financial advisors and retirement calculators use 6%-8% as the "average" return for the stock market over the "long term". "Average" means that there will be times when you gain more than 8%, and there will be times you gain less than 6%.

This is why it is EXTREMELY important to focus on minimizing your losses (The 2nd Principle of Safe Investing). This will make sure that those periods of "lower returns" are as short and small as possible.

Safe Investing Tip **Please note that these are very basic compound interest examples. The data, as well as the Rule of 72, assumes a constant interest rate (which is unlikely), reinvestment of interest/dividends, and no adjustment for taxes, fees, commissions, etc.